1. Create a public and private keypair using ECDSA. Private key, \( k\) and public key, \( P\) such that \[ P = kG\] where \( G\) is elliptic curve base point.
2. Generate a nonce keypair using ECDSA. Private nonce, \( r\) and public nonce \( R\) such that \[ R = rG\]
3. Send message \( (m)\), public nonce \( (R)\) and public key \( (P)\) to recipient.

Note: Public and private keys can be reused, but a new nonce keypair should be generated for each signature.

1. Create a challenge \( e\), \[ e = H( R || P || m )\] where \( H\) is a 256 bit hash function (SHA256)
2. Create signature \( s\), \[ s = r + ke\]

Recipient can calculate \( e\), since they already know \( m\), \( R\) and \( P\). But they don't know the private key \( (k)\) and private nonce \( (r)\).

Let's start from signature \( s\), \[ s = r + ke\] Multiply both sides by \( G\) (elliptic curve base point), \[ sG = (r + ke)G\] \[ sG = rG + (kG)e\] By substitution, \[ sG = R + Pe\] Recipient can verify this equation to verify the signature \( s\).

1. Each signer has a public and private keypair using ECDSA. Private key, \( k_i\) and public key, \( P_i\), such that, \[ P_i = k_iG\] where \( G\) is elliptic curve base point.
2. Each signer generates a nonce keypair using ECDSA. Private nonce, \( r_i\) and public nonce, \( R_i\), such that \[ R_i = r_iG\]

1. Each signer shares \( H(R_i)\) with all other participants. Here, \( H\) is a 256-bit hash function.
2. Upon receipt of \( H(R_i)\) from every other signer, each signer communicates \( R_i\) to all participants.
3. The recipient verifies that each \( R_i\) is consistent with previously communicated hash, \( H(R_i)\).

1. Each signer calculates the combined public key, \( P\), as follows: \[ \ell = H( P_1 || P_2 || \cdots || P_n )\] \[ \mu_i = H( \ell || P_i )\] where, \( \mu_i\) is MuSig coefficient. \[ P = \sum_{i = 0}^n \mu_i P_i\]
2. Each signer calculates combined nonce, \( R\), and a challenge, \( e\), as follows: \[ R = \sum_{i = 0}^n R_i\] \[ e = H( R || P || m )\] where, \( m\) is the message to be signed.
3. Each signer computes their partial signature, \( s_i\), as follows: \[ s_i = r_i + k_i \mu_i e\]
4. Complete signature is then \( (s, R)\) where \( s\) is, \[ s = \sum_{i = 0}^n s_i\]

Recipient can calculate \( e\), since they already know \( m\), \( R\) and \( P\).

Let's start from signature \( s\), \[ s = \sum_{i = 0}^n s_i\] By substitution, \[ s = \sum_{i = 0}^n ( r_i + k_i \mu_i e)\] Multiply both sides by \( G\) (elliptic curve base point), \[ sG = \sum_{i = 0}^n ( r_i + k_i \mu_i e)G\] \[ sG = \sum_{i = 0}^n r_i G + \sum_{i = 0}^n \mu_i (k_i G) e\] By substitution, \[ sG = \sum_{i = 0}^n R_i + \sum_{i = 0}^n \mu_i P_i e\] \[ sG = R + Pe\] Recipient can verify this equation to verify the signature \( (s, R)\).

Avalanche is a new family of consensus protocols inspired by gossip algorithms. The protocol is based on random sampling and meta-stable decision, and provide a strong probabilistic safety guarantee.

This protocol family achieves its properties by humbly cheating in three different ways:

1. Adopting a safety guarantee that is probabilistic.
2. Establishing only partial order between dependent transactions.
3. No liveliness guarantee for misbehaving clients.

Avalanche protocol provides the following guarantees with high probability:

• Safety: No two correct nodes will accept conflicting transactions.
• Liveliness: Any transaction issued by a correct client will eventually be accepted by every correct node.

Avalanche protocol makes following assumptions:

• A synchronous network.
• All members of a network are not known to all participants.
• A safe bootstrapping system that enables a node to connect with sufficiently many correct nodes.

Avalanche starts with a non-Byzantine protocol and progressively build on it to arrive at Byzantine Fault Tolerant (BFT) protocol. It consists of following four protocols:

1. Slush
2. Snowflake
3. Snowball
4. Avalanche

• A node starts out with an uncolored state.
• Upon receiving a transaction, an uncolored node updates its own colour to the one carried in the transaction and initiates a query.
• To perform a query, a node picks a small, constant sized \( (k)\) sample of the network uniformly at random, and sends a query message.
• Upon receiving a query, an uncolored node adopts the colour in the query, responds with that colour, and initiates its own query, whereas a coloured node simply responds with its current colour.
• Once the querying node collects \( k\) responses, it checks if a fraction \( \geq \alpha k\) are for the same colour, where \( \alpha \gt 0.5\) is a protocol parameter.
• If the \( \alpha k\) threshold is met and the sampled colour differs from the node's own colour, the node flips to that colour.
• It then goes back to the query step , and initiates a subsequent round of query, for a total of \( m\) rounds.
• Finally, the node decides the colour it ended up with after \( m\) rounds.

• Each node maintains a counter \( cnt\).
• Upon every colour change, the node resets \( cnt\) to \( 0\).
• Upon every successful query that yields \( \geq \alpha k\) responses for the same colour as the node, the node increments \( cnt\).
• A node accepts the current colour when its counter exceeds \( \beta\), another security parameter.

• Each node maintains a confidence counter.
• Upon every successful query, the node increments its confidence counter for that colour.
• A node switches colours when the confidence in its current colour becomes lower than the confidence value of the new colour.
• A node decides a colour if, during a certain number of consecutive queries, its confidence for that colour exceeds that of other colours.

• Each node maintains a dynamic append-only Directed Acyclic Graph (DAG) of all known transactions.
• The DAG has single sink that is genesis vertex.
• When a client creates a transaction, it names one or more parents, which are included inseparably in that transaction and form the edges of the DAG.

We use the term ancestor set to refer to all transactions reachable via parent edges back in history, and progeny to refer to all children transactions and their offspring.

The central challenge in the maintenance of the DAG is to choose among conflicting transactions. For example, in a cryptocurrency application, transactions that spend the same funds (double-spends) conflict, and form a conflict set, out of which only a single one can be accepted. Note that the conflict set of a correct transaction is always a singleton. Also, it is worth noting that each transaction in a conflict set may have different parent transaction (this depends on implementation of parent selection).

• When a transaction \( T\) is queried, all transactions reachable from \( T\) by following the DAG edges are implicitly part of the query.
• A node will only respond positively to the query if \( T\) and its entire ancestry are currently the preferred option in their respective conflict sets.
• If more than a threshold of responders vote positively, the transaction is said to collect a chit, \( c_{uT} = 1\), otherwise \( c_{uT} = 0\).
• Nodes then compute their confidence as the sum of chit values in the progeny of that transaction.
• Nodes query a transaction just once and rely on new vertices and chits, added to progeny, to build up their confidence.
• Ties are broken by an initial preference for the first-seen transactions.

• Each correct node \( u\) keeps track of all transactions it has learned about in a set \( \mathcal{T}_u\), partitioned into mutually exclusive conflict sets \( \mathcal{P}_T\), where \( T \in \mathcal{T}_u\). Since conflicts are transitive, if \( T_i\) and \( T_j\) are conflicting, then \( \mathcal P_{T_i} = \mathcal P_{T_j}\)
• We write \( T' \leftarrow T\) if \( T\) has a parent edge to \( T'\).
• Each node \( u\) can compute a confidence value for transaction \( T\), \( d_u(T)\), from the progeny as follows: \[ d_u(T) = \sum_{T' \in \mathcal T_u, T \xleftarrow{\ast} T'} c_{uT'} \] Above formula means that the confidence value of a transaction is sum of chits collected by its children and their off-springs (progeny).

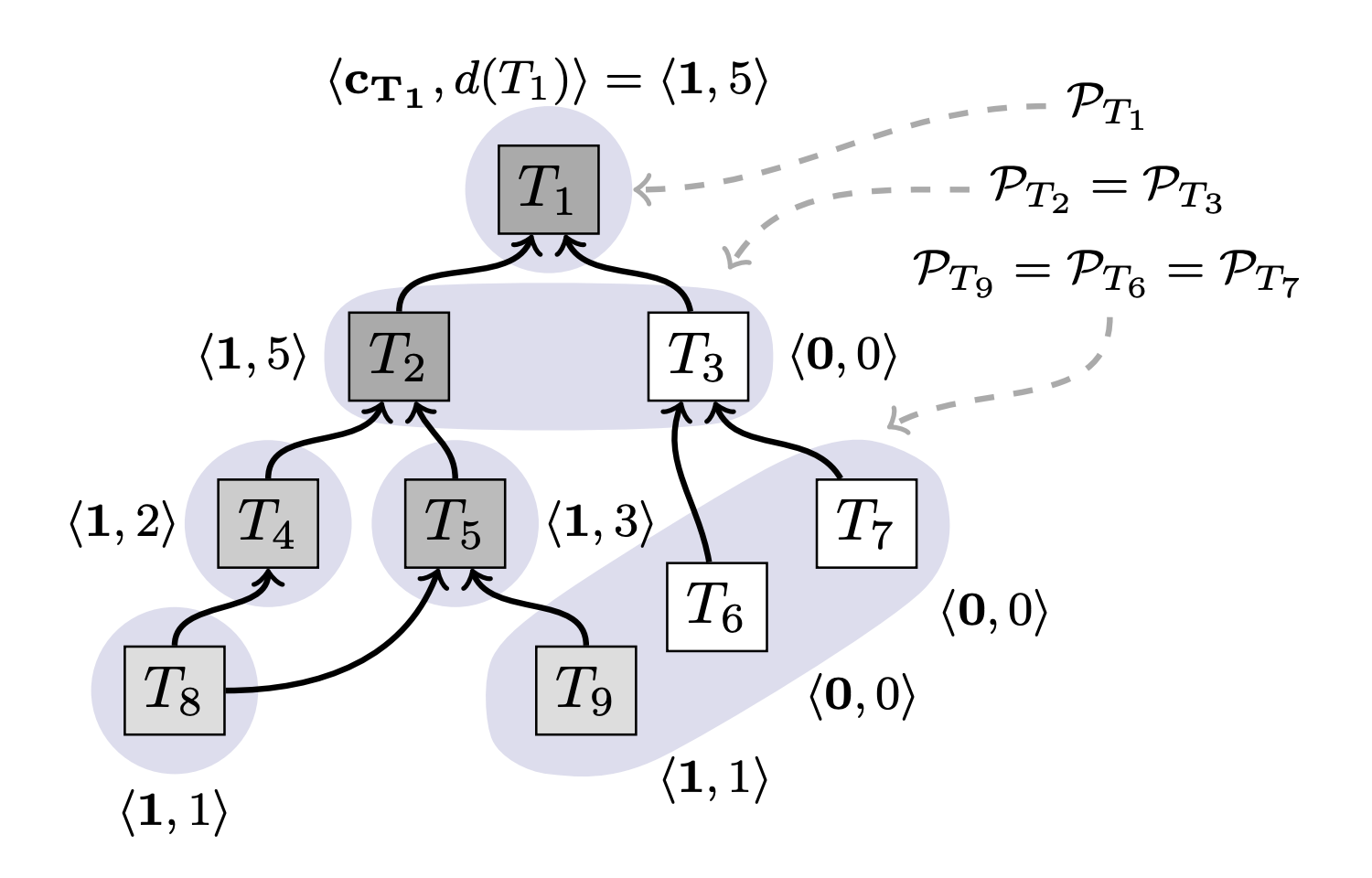
Note: Above image is just for providing an example and the values may not be accurate.

• When a node \( u\) discovers a transaction \( T\) through query, it starts a one-time query process by sampling \( k\) random peers.
• A query starts by adding \( T\) to \( \mathcal T\), initializing \( c_T\) to \( 0\), and then sending a message to selected peers.
• Node \( u\) answers a query by checking weather each \( T'\) such that \( T' \xleftarrow{\ast} T\) (i.e., every parent of \( T\)) is currently preferred among their respective conflict sets, \( \mathcal P_{T'}\).
  • If every single ancestor \( T'\) fulfills this criterion, the transaction is said to be strongly preferred, and receives a yes-vote(1).
  • A failure of this criterion at any \( T'\) yields a no-vote (0).
• When \( u\) accumulates \( k\) responses, it checks weather there are \( \alpha k\) yes-votes for \( T\), and if so grants the chit \( c_T = 1\) for \( T\).

The above mentioned process is brief of Avalanche Consensus Algorithm. To understand it fully, it is recommended to read Section 2.6 along with the pseudo-code in Avalanche Paper.

The goal of the parent selection algorithm is to yield a well-structured DAG that maximizes the likelihood that virtuous transactions will be quickly accepted by the network.

There are inherent trade-offs in the parent selection algorithm:

• Selecting well-accepted parents makes it more likely for a transaction to find support, but can lead to vote dilution.
• Selecting more recent parents at the frontier of the DAG can lead to stuck transactions, as the parents may turn out to be rogue and remain unsupported.

The adaptive parent selection algorithm chooses parents by starting at the DAG frontier and retreating towards the genesis vertex until finding an eligible parent. The eligibility criteria has following four conditions:

• Transaction should be strongly preferred, i.e., every single of its ancestor is preferred among their respective conflict sets.
• Transaction's conflict set size should be \( 1\), i.e., there should not be any conflicting transactions to current transaction.
• Transaction should have a confidence value, \( d(T) \gt 0\)
• None of this transaction's children should satisfy above three conditions.

To understand more about parent selection, it is recommended to read Section 4 along with the pseudo-code in Avalanche Paper.